Casio fx-5800P - Manuale (Pagina 67)

I-66
A Ottenimento del determinante di una matrice
La funzione det( può essere usata per ottenere il determinante di una matrice quadrata.
det a
11
= a
11
det = a
11
a
22
– a
12
a
21
a
11
a
12
a
21
a
22
det = a
11
a
22
a
33
+ a
12
a
23
a
31
+ a
13
a
21
a
32
– a
13
a
22
a
31
– a
12
a
21
a
33
– a
11
a
23
a
32
a
11
a
12
a
13
a
21
a
22
a
23
a
31
a
32
a
33
Esempio: Per ottenere il determinate della matrice
1 –2
5 0
.
Questo esempio presuppone che Mat C contenga
1 –2
5 0
.
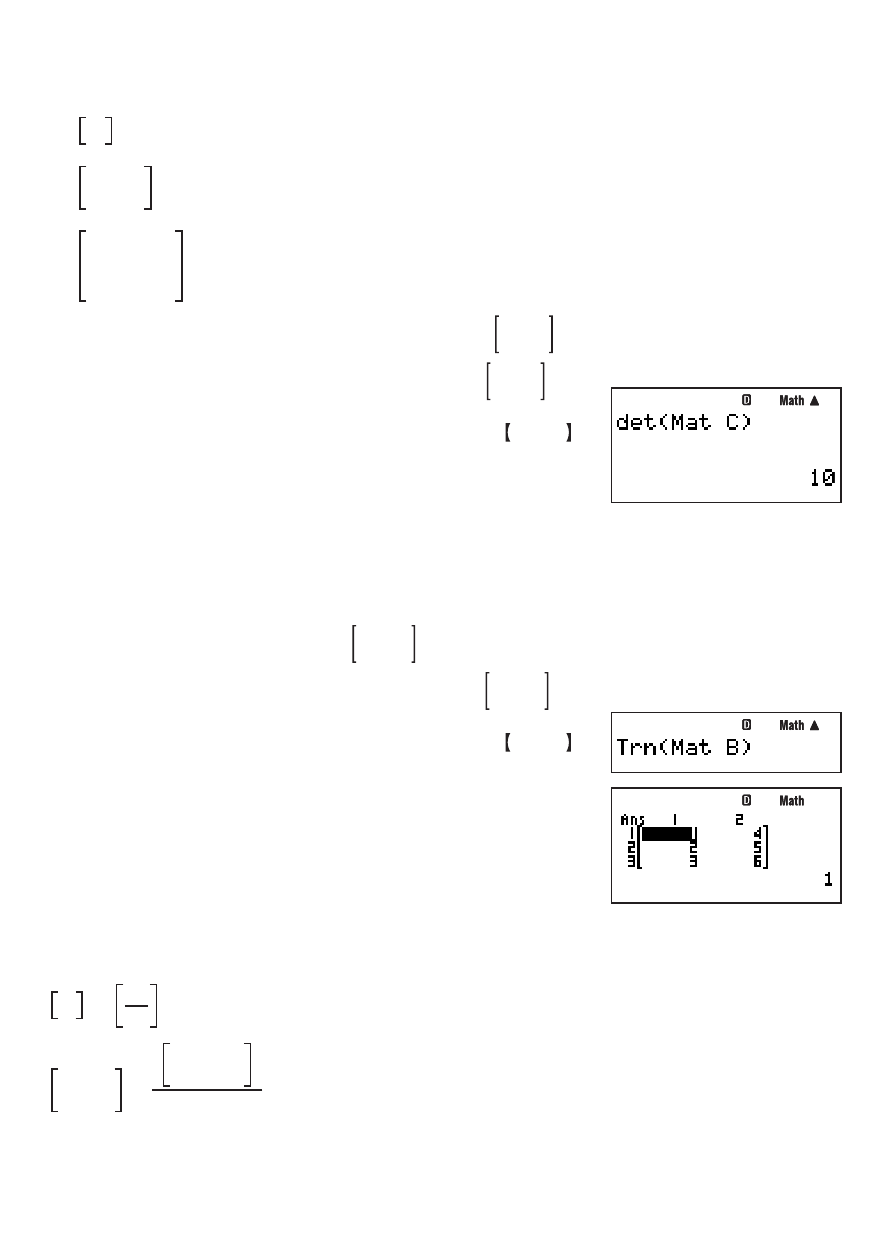
z – {MATRIX}3(det)
Mat C
)
E
A Trasposizione di una matrice
Per trasposizione di una matrice si intende fondamentalmente scambiare le sue righe in
colonne e le sue colonne in righe. Il calcolo viene eseguito usando la funzione Trn( come
mostrato sotto.
Esempio: Per trasporre la matrice
1 2 3
4 5 6
.
Questo esempio presuppone che Mat B contenga
1 2 3
4 5 6
.
z – {MATRIX}4(Trn)
Mat B
)
E
A Inversione di una matrice
È possibile usare la procedura mostrata sotto per invertire una matrice quadrata.
a
11
–1
=
a
11
1
a
11
a
12
–1
a
21
a
22
a
22
– a
12
– a
21
a
11
a
11
a
22
– a
12
a
21
=