Casio CFX-9850GB PLUS Capitolo 18 - Manuale (Pagina 53)

301
Esempio Per calcolare l’intervallo t per 1 campione per una lista di dati
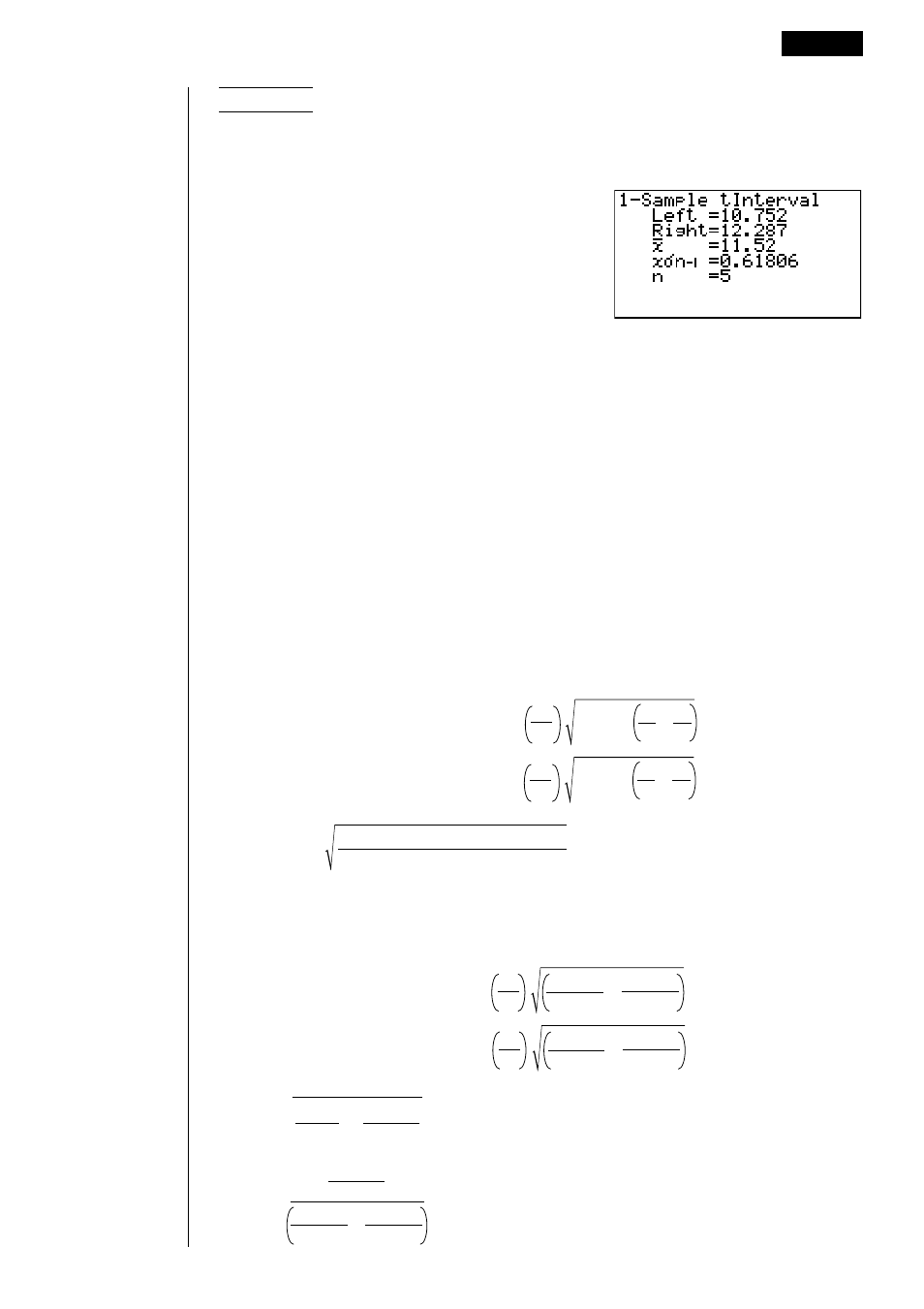
Per questo esempio, otterremo l’intervallo t per 1 campione
per i dati = {11,2, 10,9, 12,5, 11,3, 11,7} quando C-Level = 0,95.
1(List)c
a.jf
w
1(List1)c
1(1)c
1(CALC)
Left ................. Limite inferiore dell’intervallo (margine sinistro)
Right ............... Limite superiore dell’intervallo (margine destro)
o ..................... Media del campione
x σ
n -1
................ Deviazione standard del campione
n ..................... Dimensione del campione
u uu u uIntervallo t per 2 campioni
L’intervallo t per 2 campioni calcola l’intervallo di confidenza per la differenza tra
due medie di popolazione, quando entrambe le deviazioni standard della
popolazione sono sconosciute. L’intervallo
t è applicato alla distribuzione t .
Il seguente intervallo di confidenza vale quando il raggruppamento è in vigore.
Il valore 100 (1–
α ) % è il livello di confidenza.
Il seguente intervallo di confidenza vale quando il raggruppamento non è in
vigore.
Il valore 100 (1–
α ) % è il livello di confidenza.
C =
df =
1
C 2
n
1
–1
+
(1–C ) 2
n
2
–1
+
n
1
x
1 n–1
2 σ
n
1
x
1 n–1
2 σ
n
2
x
2 n–1
2 σ
Left (sinistra) = ( o
1
– o
2
)– t
df
α
2
Right (destra) = ( o
1
– o
2
)+ t
df
α
2
+
n
1
x
1 n–1
2 σ
n
2
x
2 n–1
2 σ
+
n
1
x
1 n–1
2 σ
n
2
x
2 n–1
2 σ
Left (sinistra) = ( o
1
– o
2
)– t
α
2
Right (destra) = ( o
1
– o
2
)+ t
α
2
n
1
+n
2
–2 n
1
1 +
n
2
1
x
p n –1
2
σ
n
1
+n
2
–2 n
1
1 +
n
2
1
x
p n –1
2
σ
Intervallo di confidenza
18 - 7
x
p n –1
= σ
n
1
+ n
2
– 2
(n
1
–1)x
1 n –1
2 +(n
2
–1) x
2 n –1
2 σ σ